一、一次函數的概念
若兩個變量像x、y的關系,可以表示成:y=kx+b(k,b為常數,且k≠0)的形式;那么y就叫做x的一次函數;其中,x是自變量,y是因變量。
1.一次函數的解析式的形式是y=kx+b,判斷一個函數是否是一次函數,就是判斷是否能化成以上形式。
2.當b=0,k≠0時,y=kx 仍是一次函數。
3.當b=0,k=0時,它不是一次函數。
4.正比例函數是一次函數的特例,一次函數包括正比例函數。
二、一次函數的圖象和性質
1. 圖象
2. 性質
①在一次函數上的任意一點P(x,y),都滿足等式:y=kx+b。
②直線 y=kx+b與y軸的交點是(0,b),與x軸的交點是
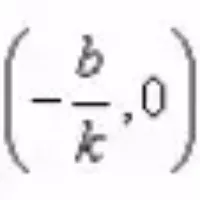
③正比例函數的圖象總是過原點。
三、正比例函數與一次函數之間的關系
一次函數y=kx+b的圖象是經過(0,b)和
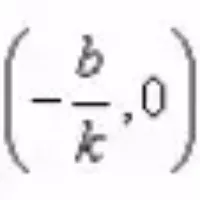
兩點的一條直線,我們稱它為直線y=kx+b,它可以看作由直線 y=kx平移 |b| 個單位長度得到。(當b>0時,向上平移;當b<0時,向下平移)
四、用待定系數法確定函數解析式的一般步驟
已知點A(x₁,y₁),B(x₂,y₂),請確定過點A,B的一次函數的表達式。
(1)設一次函數的表達式(也叫解析式)為y=kx+b。
(2)因為在一次函數上的任意一點P(x,y),都滿足等式 y=kx+b。所以可以列出2個方程:
y₁=kx₁+b…....①
y₂=kx₂+b.......②
(3)解這個二元一次方程,得到k、b的值。
(4)最后得到一次函數的表達式。
五、直線的平移
直線 y=kx+b 向上平移 m(m>0)個單位長度得到直線y=kx+b+m;
直線 y=kx+b 向下平移 m(m>0)個單位長度得到直線 y=kx+b-m;
直線 y=kx+b 向左平移 m(m>0)個單位長度得到直線 y=k(x+m)+b;
直線 y=kx+b 向右平移m(m>0) 個單位長度得到直線y=k(x一m)+b。
直線平移的規律用八字口訣來形象表示:上加下減,左加右減。
六、直線y=k?x+b?(k?≠0)與y=k?x+b?(k?≠0)的位置關系
(1)兩直線平行,可得 k?=k? 且 b?≠b?
(2)兩直線相交,可得 k?≠k?
(3)兩直線重合,可得 k?=k? 且 b?=b?
(4)兩直線垂直,可得 k?k?= -1
七、常用公式
歡迎使用手機、平板等移動設備訪問中考網,2025中考一路陪伴同行!>>點擊查看