來源:網(wǎng)絡(luò)資源 2022-10-10 16:39:13
一、相似、全等的關(guān)系
全等和相似是平面幾何中研究直線形性質(zhì)的兩個重要方面,全等形是相似比為1的特殊相似形,相似形則是全等形的推廣.因而學(xué)習(xí)相似形要隨時與全等形作比較、明確它們之間的聯(lián)系與區(qū)別;相似形的討論又是以全等形的有關(guān)定理為基礎(chǔ).
二、相似三角形
(1)三角形相似的條件:
①;②;③.
三、兩個三角形相似的六種圖形:
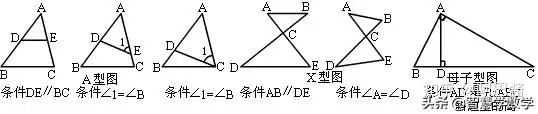
四、三角形相似的證題思路:判定兩個三角形相似思路:
1)先找兩對內(nèi)角對應(yīng)相等(對平行線型找平行線),因為這個條件最簡單;
2)再而先找一對內(nèi)角對應(yīng)相等,且看夾角的兩邊是否對應(yīng)成比例;
3)若無對應(yīng)角相等,則只考慮三組對應(yīng)邊是否成比例;

五、“三點(diǎn)定形法”,即由有關(guān)線段的三個不同的端點(diǎn)來確定三角形的方法
例1、已知:如圖,ΔABC中,CE⊥AB,BF⊥AC.
求證:
![]()
例2、如圖,CD是Rt△ABC的斜邊AB上的高,∠BAC的
平分線分別交BC、CD于點(diǎn)E、F,AC·AE=AF·AB嗎?
說明理由。
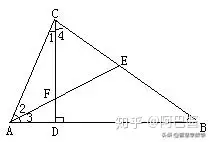
分析方法:
1)先將積式______________
2)______________( “橫定”還是“豎定”? )
六、過渡法(或叫代換法)
有些習(xí)題無論如何也構(gòu)造不出相似三角形,這就要考慮靈活地運(yùn)用“過渡”,其主要類型有三種,下面分情況說明.
1、 等量過渡法(等線段代換法)
遇到三點(diǎn)定形法無法解決欲證的問題時,即如果線段比例式中的四條線段都在圖形中的同一條直線上,不能組成三角形,或四條線段雖然組成兩個三角形,但這兩個三角形并不相似,那就需要根據(jù)已知條件找到與比例式中某條線段相等的一條線段來代替這條線段,如果沒有,可考慮添加簡單的輔助線。然后再應(yīng)用三點(diǎn)定形法確定相似三角形。只要代換得當(dāng),問題往往可以得到解決。當(dāng)然,還要注意最后將代換的線段再代換回來。
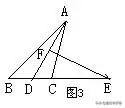
例1:如圖3,△ABC中,AD平分∠BAC, AD的垂直平分線FE交BC的延長線于E.求證:DE2=BE·CE.
分析:
1、 等比過渡法(等比代換法)
當(dāng)用三點(diǎn)定形法不能確定三角形,同時也無等線段代換時,可以考慮用等比代換法,即考慮利用第三組線段的比為比例式搭橋,也就是通過對已知條件或圖形的深入分析,找到與求證的結(jié)論中某個比相等的比,并進(jìn)行代換,然后再用三點(diǎn)定形法來確定三角形。
例2:如圖4,在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中點(diǎn),ED交AB的延長線于點(diǎn)F.
求證:
![]()

3、等積過渡法(等積代換法)
思考問題的基本途徑是:用三點(diǎn)定形法確定兩個三角形,然后通過三角形相似推出線段成比例;若三點(diǎn)定形法不能確定兩個相似三角形,則考慮用等量(線段)代換,或用等比代換,然后再用三點(diǎn)定形法確定相似三角形,若以上三種方法行不通時,則考慮用等積代換法。
小結(jié):證明等積式思路口訣:“遇等積,化比例:橫找豎找定相似;
不相似,不用急:等線等比來代替。”
七、證比例式和等積式的方法:
對線段比例式或等積式的證明:常用“三點(diǎn)定形法”、等線段替換法、中間比過渡法、面積法等.若比例式或等積式所涉及的線段在同一直線上時,應(yīng)將線段比“轉(zhuǎn)移”(必要時需添輔助線),使其分別構(gòu)成兩個相似三角形來證明.
可用口訣:遇等積,改等比,橫看豎看找關(guān)系; 三點(diǎn)定形用相似,三點(diǎn)共線取平截;
平行線,轉(zhuǎn)比例,等線等比來代替; 兩端各自找聯(lián)系,可用射影和園冪.
例1 如圖5在△ABC中,AD、BE分別是BC、AC邊上的高,DF⊥AB于F,交AC的延長線于H,交BE于G,求證:(1)FG/FA=FB/FH(2)FD是FG與FH的比例中項.
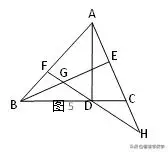
1說明:證明線段成比例或等積式,通常是借證三角形相似.找相似三角形用三點(diǎn)定形法(在比例式中,或橫著找三點(diǎn),或豎著找三點(diǎn)),若不能找到相似三角形,應(yīng)考慮將比例式變形,找等積式代換,或直接找等比代換
八、確定證明的切入點(diǎn)。幾何證明題的證明方法主要有三個方面。第一,從“已知”入手,通過推理論證,得出“求證”;第二,從“求證”入手,通過分析,不斷尋求“證據(jù)”的支撐,一直追溯回到“已知”;第三,從“已知”及“求證”兩方面入手,通過分析找到中間“橋梁”,使之成為清晰的思維過程。
九、相似三角形中的輔助線
在添加輔助線時,所添加的輔助線往往能夠構(gòu)造出一組或多組相似三角形,或得到成比例的線段或得出等角,等邊,從而為證明三角形相似或進(jìn)行相關(guān)的計算找到等量關(guān)系。主要的輔助線有以下幾種:
一、作平行線
二、作延長線
三、作中線
歡迎使用手機(jī)、平板等移動設(shè)備訪問中考網(wǎng),2025中考一路陪伴同行!>>點(diǎn)擊查看