2023年初中數(shù)學(xué)四邊形綜合題

【例題】

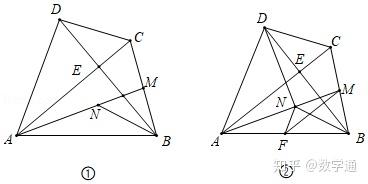
如圖①，在四邊形ABCD中，AC⊥BD于點(diǎn)E，AB=AC=BD，點(diǎn)M為BC中點(diǎn)，N為線段AM上的點(diǎn)，且MB=MN

(1)求證：BN平分∠ABE;

(2)若BD=1，連接DN，當(dāng)四邊形DNBC為平行四邊形時(shí)，求線段BC的長(zhǎng);

(3)若點(diǎn)F為AB的中點(diǎn)，連接FN、FM(如圖②)，求證：∠MFN=∠BDC.

【考查知識(shí)點(diǎn)】四邊形綜合題;幾何綜合題

【解題分析】

(1)由AB=AC知∠ABC=∠ACB，由等腰三角形三線合一知AM⊥BC，從而根據(jù)∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC，再由△MBN為等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°就可以證明;

(2)設(shè)BM=CM=MN=a，知DN=BC=2a，證△ABN≌△DBN得AN=DN=2a，Rt△ABM中利用勾股定理可得a的值，從中得出答案;

(3)F是AB的中點(diǎn)知MF=AF=BF及∠FMN=∠MAB=∠CBD，再由MF/AB=MN/BC=1/2，即MF/BD=MN/BC，得△MFN∽△BDC，即可得證.

【詳細(xì)解答】

(1)證明：如圖①，∵AB=AC，

∴∠ABC=∠ACB，

∵M(jìn)是BC的中點(diǎn)，

∴AM⊥BC，

在Rt△ABM中，∠MAB+∠ABC=90°，

在Rt△CBE中，∠EBC+∠ACB=90°，

∴∠MAB=∠EBC，

∵M(jìn)B=MN，

∴△MBN是等腰直角三角形，

∴∠MNB=∠MBN=45°，

∵∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°，

∴∠NBE=∠ABN，即BN平分∠ABE;

(2)解：設(shè)BM=CM=MN=a，

∵四邊形DNBC是平行四邊形，

∴DN=BC=2a，

在△ABN和△DBN中，

∵AB=DB,角NBE=角ABN，BN=BN

∴△ABN≌△DBN(SAS)，

∴AN=DN=2a，

在Rt△ABM中，由AM2+MB2=AB2，可得：(2a+a)2+a2=1，

解得：a=±根號(hào)10/10(負(fù)值舍去)，

∴BC=2a=根號(hào)10/5;

(3)解：∵F是AB的中點(diǎn)，

∴在Rt△MAB中，MF=AF=BF，

∴∠MAB=∠FMN，

∵∠MAB=∠CBD，

∴∠FMN=∠CBD，

∵M(jìn)F/AB=MN/BC=1/2，即MF/BD=MN/BC，

∴△MFN∽△BDC，

∴∠MFN=∠BDC.

【總結(jié)】

這道題屬于四邊形的綜合題，解決這道題目的關(guān)鍵是掌握等腰三角形三線合一的性質(zhì)、直角三角形和平行四邊形的性質(zhì)及全等三角形與相似三角形的判定與性質(zhì)等知識(shí)點(diǎn)，如果掌握這些知識(shí)點(diǎn)，那么解決起來(lái)就不難了。

　　 歡迎使用手機(jī)、平板等移動(dòng)設(shè)備訪問(wèn)中考網(wǎng)，2025中考一路陪伴同行！>>點(diǎn)擊查看