2023年初中數學反比例函數突破方法

我們先來看例題，最后會給大家總結反比例函數如何破題。

題目我們先易后難!

例題1：代表一類反比例函數定性分析題

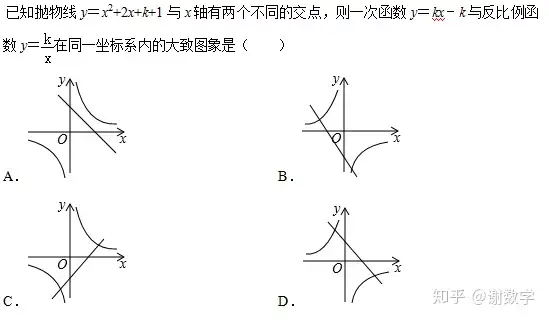
這類題目屬于定性分析題，不要你實實在在算出具體數字的題目。但是要做對，也是需要你對反比例函數定義以及拋物線定義有所了解。這題不是單純只考反比例函數內容還結合了拋物線知識。屬于雙線結合題。出題遵循先易后難，放在例題1，說明難度不大。拋物線有兩個不同交點，說明▲=b²-4ac>0可以得到。計算出K<0反比例過二、四象限。直接排除A、C兩個選項。接下來y=kx-k說明這個函數必過(1、0)點所以直接選D選項。如何理解必過(1.0)點，這個知識點經常考。y=kx-k=k(x-1) 當x取1時，無論K為何值。y必然為0 所以必過(1.0)點。

例題2：代表一類可求X與y分別是多少的反比例函數題

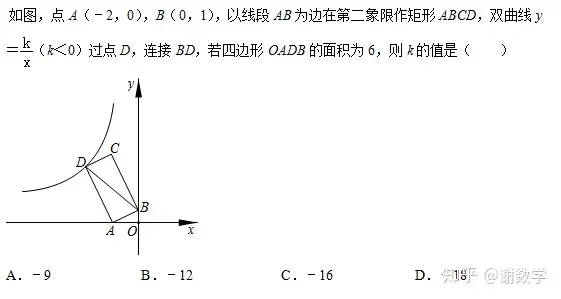
例題2難度不是很大。四邊形OADB面積為6，四邊形OADB是個不規則圖形。那么不規則圖形的面積計算方法必然是用割補法。很明顯這個S圖形OADB=S▲AOB+S▲ABD 因為S▲AOB=1則S▲ABD=5 2分之1的AB乘以AD等于5。接下來AB的長我們知道為 根號5 所以AD長為 2又根號5 當我們得到AD長以后。有什么作用呢?接下來就要說解反比例函數的思路了。反比例函數題大概率是求K值，求K值我們必然要聯系到K=xy 這個代數式，那么要求K值必然要求xy相乘為多少。那么是不是分兩種情況!!!

一種情況：我們可以單獨求出X和Y各是多少。然后最后相乘求K

另外一種情況:題目無法求出X和Y各是多少，只能求出XY相乘的積是一個定值。那么積也是K

當你分清楚這兩個問題后，再思考!要求X和Y其實質就是求線段的長度，那么是不是要做反比例函數上的點垂直X 軸和垂直Y軸的輔助線?所以出現反比例函數題目，不管你會不會做，先找反比例函數上的點做垂直X 軸和垂直Y軸的輔助線!!!

做完輔助線后必然的步驟就是求線段的長度了!!!那么求線段的長度也是我們經常遇到的數學題。求線段長度的方法有哪些呢?再我還沒寫出來的時候自己腦袋再思考思考。

想到了嗎?

求線段長度經常用的方法有以下幾種：

1、三角函數法：

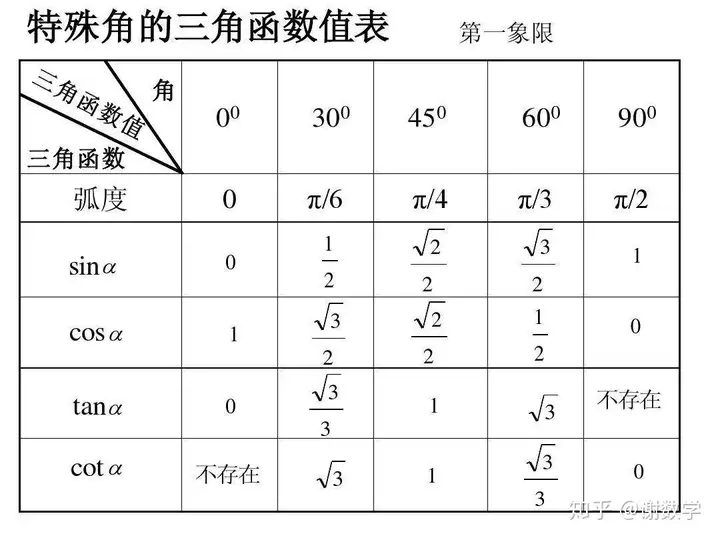
有涉及三角函數的必須是要在直角三角形里面去做。普通三角形給你其中一個內角是特殊角是沒有任何意義的。因此要使用三角函數法求線段長度，也是需要在直角三角形里面找線段直接比例的。如果沒有直角三角形，但是出現了上圖的特殊角看看能不能構造直接三角形。

2、勾股定理：

這個方法始終貫穿我們初中階段。

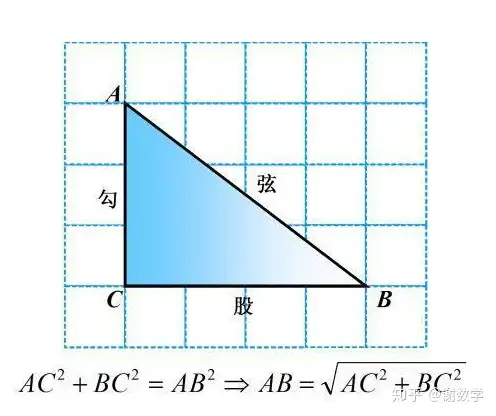
3、全等三角形的判定方法。(SSS/SAS/ASA/AAS/HL)五種判定全等三角形的方法記住了沒有?

4、用證明相似三角形的方法求知線段的長度。

只要是用相似三角形的方法求線段長度，那么經常遇到如下模型：

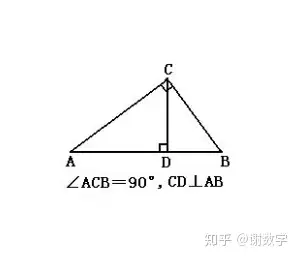
大直角三角形套小直角三角形模型簡稱大套小

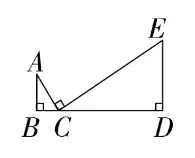
K模型

就是三個直角三角形兩兩相似的模型。

延伸了那么多題外知識點，我們回到剛才的題目。當你算出AD長為 2又根號5之后，所以你要想到做D點垂直X軸。然后得到了上面的K模型。

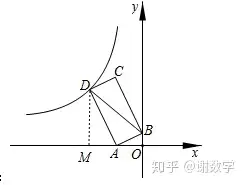
再用勾股定理求X=2因此 xy=16 記住經過二四象限K值為負數。最終答案為-16選C

例題3：代表一類含有2個反比例函數同時出現的題目

含有2個反比例函數的題目相對而言，會簡單一定。這類題目考察的實質是。要會設點。

這個題目相對來說簡單一點。

例題4：代表一類無法求X和Y各是多少的。可以求xy相乘是定值的題目

梯形OACB面積為4，梯形是規則圖形，要把他們的面積表達式寫出來的第一步。

第二步，不管會不會做，先做反比例函數上的點到X軸和Y軸的輔助線。

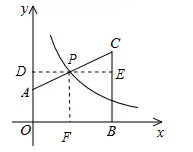
一步一步推理，答案就出來了。

例題5：代表一類反比例函數取值范圍的題目

這類題目相對來說，你只要學一次，以后遇到都會做的類型。不比上面要思考好幾個步驟，又要結合到全等，相似的題目，那么復雜。深刻理解有交點是什么意思。有沒有交點幾何意義其實就是平移反比例函數取只有一個交點時候就是臨界點。那么很明顯，A點就是最左邊的臨界點。因此K值必然最小值是2。那么最大值呢?其實就是反比例函數和線段BC只有一個交點的時候。

答案選A 這題你要學會把如何快速求K 的方法背下來。遇到這種知道平面直角坐標系上任意兩點的可以迅速求出K值。

例題6：代表滿足某種條件的定值面積的題型

這類題目看起來是很可怕的，但是實質這類題目當你學完我說的方法后，你會覺得太好用了。這類題目以后遇到再也不怕了!是不是覺得我說得神乎奇神?有點黃婆賣瓜，自賣自夸。步入正題。這類題目特征是什么?就是曲線上一個動點。看起來好可怕!反比例靜止的定要求，我都怕。還來動點!不好意思，再下告辭。不!老鄉別走。我take you fly

題目說P點是動點，實質就是無論P點如何運動，題目中要我們求的S▲POA必然是定值。那么圖中有一個特殊點，就是P點運動到C2曲線和y 軸交點的位置時。是不是就可以運用到我們所學的萬年勾股定理去求解了?有學生問，老師為什么要這樣做?不好意思，如果不這樣做。隨便取任意一點求面積的話。華佗在世也解不了!(因為華佗是學醫的，所以解不了)那么華羅庚會不會，我就不懂了。

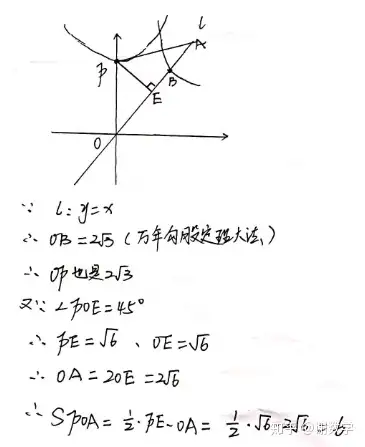
答案是：B

現在還覺得這類反比例函數動點可怕嗎?記住方法找特殊點。千萬別被出題老師思維帶跑偏了。出題老師說動點，你真的去隨便找一個點然后做輔助線。然后就沒有然后了，根本沒辦法算。

例題7：代表反比例函數題中難度指數4顆星★★★★結合了多個知識點

首先我要告訴你的是，當題目中有看到中點字眼的題目，一定要想到三個常用關系式。

一是直角三角形，斜邊上的中點。那么中線會等于斜邊的一半。

二是想到如果題目中有A(x1.y1)和B(x2.y2)這兩個點的坐標，那么AB線段的中點C橫坐標為2分之x1+x2 ，C的縱坐標為2分之y1+y2

三是要想到三角形的中位線。

那么這個題目運用到的是哪個呢?很明顯是第三個了。如何理解OQ最大值為2分之3是這個題目的解題關鍵。反比例函數是關于原點對稱的點對稱圖形，所以只要是y=kx的函數必然會被反比例函數分成三段。其中AO=BO 是一定的。這個必須當做知識點背下來。Q又是AP的中點 。因此能得到OQ就是三角形APB的中位線。那么OQ取最大值，必然就是BP取最大值。然后根據題目意思可得。P點是圓上運動的動點，B是固定的點。要使得BP 最大，BP一定要過圓心C點。那么圖就可如下圖所畫。

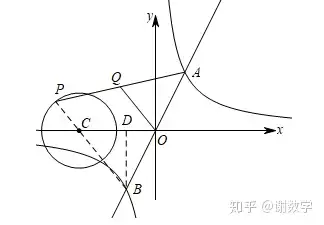
然后又回到剛才所說的，要求K，不管會做不會做，先找反比例函數上的點做垂直X軸和Y軸。那么這個題目中有兩個點在反比例函數上。是A還是B?閉上眼睛也要選B?why

A點和B點誰的已知量更多?必然是B啦!(這就是解題思路)

又變成求線段長度的問題了。上面已經說了，求線段長度就那么4種常用的。這個題目用什么?勾股定理!why ?

因為整個題目做下來你是不是發現題目中還有一個已知條件沒有用?一次函數y=2x

說到這里補充一個知識點，當你看y=x或者y=2x或者y=3x這樣的一次函數。其實實質告訴你幾何意義是這個函數和X軸構成的直角三角形的y/x比值是多少。然后可得到BD比OD在這個題目中等于2。接下來。設OD=X則BD=2X 則CD=2-X 又因為BP最大為3 所以BC為2 得到萬年勾股大法：CD²+BD²=BC² 可解X=4/5 y=2x=8/5 K值=32/25 選C

例題8：這個題目代表一類知邊長求面積比后解K值

我們看但C始終在雙曲線上運動，是不是又是有點類似上面例題6，滿足某種條件下。K值始終是一個定值。類似滿足某種條件下，面積是個定值。有點神似!第一步。要干嘛?會做不會做，先把C垂直與x 軸和Y軸輔助線做了!!!!已經強調好幾遍了，記到腦海里。

反比例函數和經過原點的kx=y又出現了。說明要想到AO=OB。題目中又有交代▲ABC為等腰三角形。又告訴你∠ACB=120°那么肯定要把OC連起來。自然而然的事情。因為120不屬于上面所說的特殊角。60度才是特殊角度。

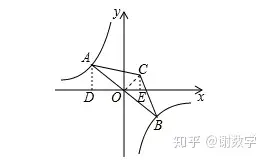
那么輔助線就是如圖所示。如果你沒有做出這個輔助線，一定要好好思考為什么自己的反比例函數解題思路沒有形成。同時也希望看完我的思路能變成自己的。這次是你看這篇文章的用處。同時更希望學有所成，能將方法用到你接下來的中考里面。

做完輔助線我們發現，題目又回到上面我所說的K模型來了。出現了RT▲ADO RT▲AOC RT▲OEC 但是我們發現。整個題目是不是沒有告訴你任何一邊的長度?沒有告訴我們任何一邊的長度，那么我們要求K值，必然無法單個求X和單個Y值是多少。所以必然用第二種求K值的方法，就是求出xy相乘的值多少也可以做。

有三個RT▲相似，先把比例寫出來。

相似三角形面積比等于邊長比的平方

這當做定理背下來，對你解題非常有幫助。再補充個題外的。相似體的體積比等于邊長比的3次方。

是不是有點不可思議的解題方法!嘆為觀止的感覺!

反比例函數題目很多，但是題型解題方法其實基本上就是上面幾個類。當然反比例函數的難題也不僅僅是這幾種。還有很多難度指數為5顆星★★★★★的題目，簡單放個下面5顆星的題目給大家。大家有空可以嘗試做一做。

這題答案為2

學完上面的方法，反比例函數題目。相信你們也不會看到就怕了。起碼覺得有思路去破題。要學會總結平常自己遇到的題目。題目是海量的，題型其實是有限。考來考去，他們萬變不離其宗。還有一個需要跟大家分享的：反比例函數如果出現整個題目只出現一個數字的!!!這類題實在不會做。你猜答案只能猜3個數字。

一是 : 數字本身。

二是：數字的2分之一。

三是：數字的2倍。

反比例函數大概率會附帶圖。具體數字是哪個?那么你要看圖中給的數字線段的長度和要求的是什么結合起來。希望這個方法能在你實在想不出的時候幫你拿到分數。好比例題4.不會做!!!你猜也只能是4或者2梯形OACB面積為4。那么大的面積才為4 那么2的概率就更大了。這是解題技巧的問題。為什么會這樣!!這是老師多年教學總結出來的經驗之談。

　　 歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看