2023年初中數學三角形內接正方形的常規解法和秒殺方法講解

初中幾何中，三角形內接四邊形是經常考到的題型，一般是內接平行四邊形、矩形、正方形等，常規思路是把要求的邊長x設出來，利用相似三角形，構造關于x的方程，從而求出x的值。

例題：

如圖，△ABC內接正方形DEFG，△AGF、△FEC、△BDG的面積分別是1、1、3，則正方形DEFG的邊長為 _

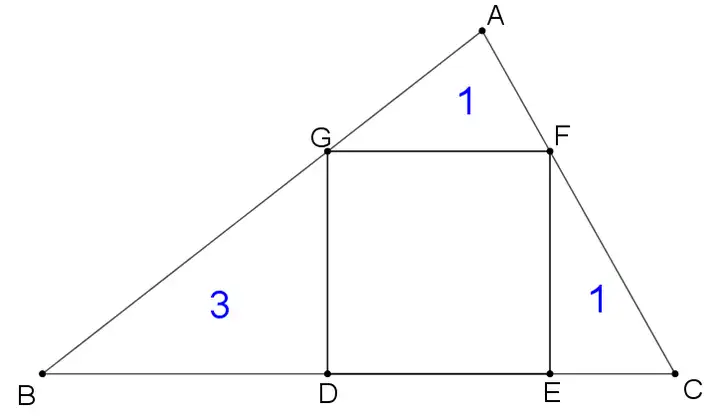
分析：按照常規思路，把正方形邊長設為x，利用△AGF∽△ABC，高之比等于邊長之比，構建關于x的方程解出x的值。

所以，

GF=x

BD=6/x

DE=x

EC=2/x

現在已經得到GF和BC的長，還需要另外一組對應邊或者對應高之比。

題目中，△AGF的面積=△EFC的面積，GF=EF，可以得到△AGF中GF邊上的高等于EC=2/x 。

那就可以利用△AGF∽△ABC，高之比等于GF與BC之比，構建關于x的方程求解。

現在講解一下秒殺方法，對于三角形內接平行四邊形問題，平行線分割成的三部分面積有一個等量關系。

感興趣的同學思考下如何證明!

(提示：相似三角形面積之比等于相似比的平方)

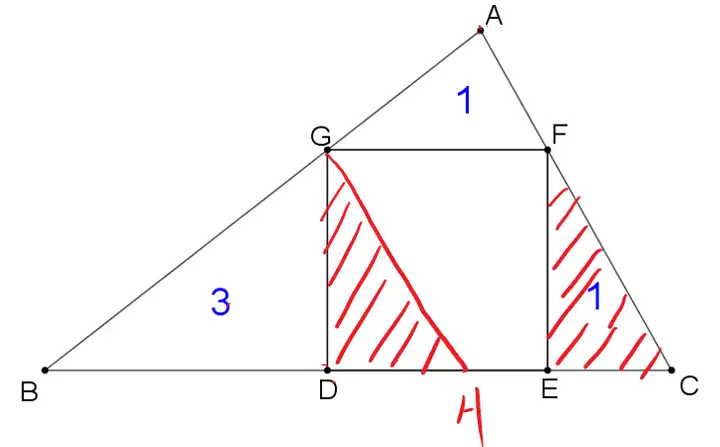
這個題就可以采用上面介紹的方法秒殺。

過點G做GH平行AC，交BC邊于點H

易證△GDH≌△FEC，

則△BGH的面積為1+3=4

平行四邊形GHCF的面積=2×√(1×4)=4

正方形GDEF的面積=平行四邊形GHCF的面積=4

所以正方形邊長為2

　　 歡迎使用手機、平板等移動設備訪問中考網，2023中考一路陪伴同行！>>點擊查看