2023年初中數(shù)學知識點：三角形的三條線段

三角形的三條線段

高：三角形的身高

每一個三角形中都有三條高，高與連接的頂點對邊存在著垂直的位置關(guān)系。根據(jù)三角形的分類，我們通過作圖的方式可以理解：

(1)銳角三角形的三條高都存在于三角形內(nèi);

(2)鈍角三角形的三條高不交于一點，只有一=條在三角形內(nèi)部，另外兩條與其延長線相交;

(3)直角三角形的三條高線交于一點，一條高線位于圖形內(nèi)部，其他兩條在直角邊上。

中線：三角形的重心

(1)每一個三角形內(nèi)有三條中線，這三條中線的交點叫做“重心”

(2)重心到頂點的距離與重心到對邊重點的距離之比為2：1

(3)重心和三角形的頂點組成的三個三角形面積相等

(4)重心到三角形三個頂點的距離平方和最小

(5)在直角坐標系中，重心的坐標是頂點坐標的算術(shù)平方根

(6)重心是三角形內(nèi)到三邊距離之積最大的點

角平分線：三角形的內(nèi)心

(1)每一個三角形也有三條角平分線，這三條角平分線的交點叫做“內(nèi)心”

(2)內(nèi)心到三角形三邊的距離相等

常見應用類型

類型一：三角形角平分線和高、中線定義的直接應用

該類型主要考察對知識點的掌握能力和運算能力，出題類型主要以選擇題和解答題的形式出現(xiàn)，難易程度一般，可直接會根據(jù)定義、性質(zhì)等做出推算。對于高和中線的應用多與角平分線進行結(jié)合出題，單獨考察時要明晰高和中線的作圖方式即可。

如圖所示，在△ABC中，D，E，F(xiàn)是BC邊上的三點，且∠1=∠2=∠3=∠4，AE是哪個三角形的角平分線( )

A.△ABE B.△ADF

C.△ABC D.△ABC，△ADF

【分析】根據(jù)三角形的角平分線的定義得出.

【解答】解：∵∠2=∠3，

∴AE是△ADF的角平分線;

∵∠1=∠2=∠3=∠4，

∴∠1+∠2=∠3+∠4，即∠BAE=∠CAE，

∴AE是△ABC的角平分線。

故選：D。

類型二：三角形的角平分線與高線相結(jié)合求角的度數(shù)

角平分線與高的結(jié)合應用是三條線段中的常見出題類型，通常題目要求算角的大小或者各角進行對比及角之間不等的運用，多以證明題的形式出現(xiàn)。要注意題目給出已知條件，從而分析角平分線、高等要素中關(guān)系。

如圖，在△ABC中，AD是高，AE是∠BAC的平分線，∠B=70°，∠C=34°，求∠DAE的大小.

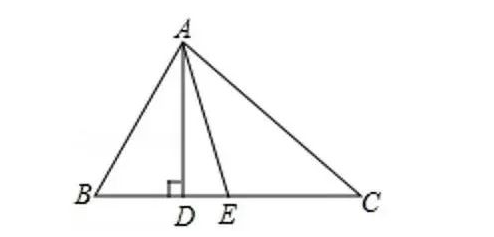
【分析】根據(jù)三角形內(nèi)角和定理求得∠BAC的度數(shù)，則∠EAC即可求解，然后在△ACD中，利用三角形內(nèi)角和定理求得∠DAC的度數(shù)，根據(jù)∠DAE=∠DAC-∠EAC即可求解.

類型三：求三角形兩內(nèi)角平分線相交所成角的度數(shù)

在三角形的三條線段中，角平分線經(jīng)常作為考點和要點出現(xiàn)在試題中，進行角與角、角與線段、線段與線段之間的比較。

如圖，△ABC中，BE，CD為角平分線且交點為點O，當∠A=60°時，

(1)求∠BOC的度數(shù);

(2)當∠A=100°時，求∠BOC的度數(shù);

(3)若∠A=α°時，求∠BOC的度數(shù).

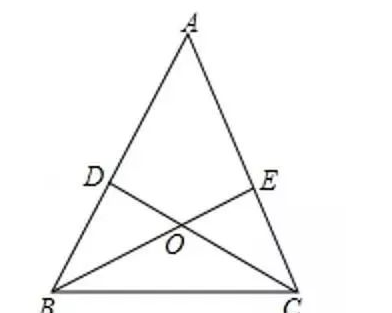
【分析】(1)在△ABC中利用三角形內(nèi)角和定理和角平分線的定義可求得∠OBC+∠OCB，在△BOC中利用三角形內(nèi)角和定理可求得∠BOC;(2)方法同(1);(3)方法同(1)。

三角形的重心和內(nèi)心主要放在有關(guān)向量和圓的應用學習中，后續(xù)更新將會涉及到詳細內(nèi)容……

數(shù)學的學習要全面回歸課本，把書上的概念、性質(zhì)、公式、定理以及銜接知識、拓展知識進行整理、歸納，形成知識網(wǎng)絡，然后轉(zhuǎn)化思想，運用到實際的題型中，這才是高效有用的學習方法。

三角形是初中數(shù)學中幾何部分的基礎(chǔ)圖形，在牢固掌握基礎(chǔ)知識的前提下，要積極探索其中的知識奧秘，這樣才能有便于后續(xù)其他幾何圖形的學習和應用。

     編輯推薦：

      2023年中考各科目重點知識匯總

　　 歡迎使用手機、平板等移動設備訪問中考網(wǎng)，2023中考一路陪伴同行！>>點擊查看