來源:網絡資源 2023-02-03 20:09:17
兩圓一線
一線,指的是線段的中垂線;
兩圓,指的是以線段長度為半徑,線段端點為圓心而產生的兩個圓。
首先,我們來解決第一個問題,等腰三角形的生成問題。
在平面內有一線段AB,點C為平面內任意一點,若△ABC為等腰三角形,則這樣的點C有幾個?點C的軌跡又是什么?根據等腰三角形的性質,線段AB有可能為底邊,也有可能為腰,故有兩種基本情況。:線段AB為底邊,則有AC=BC,即點C到線段AB兩端點的距離相等,故點C在線段AB的中垂線上,此時點C有無數個,點C的軌跡為直線(不取與AB相交的點),如下圖:
情況(2)
:線段AB為腰,則有:①AB=AC,即點C到點A的距離等于點B到點A的距離,則點C在以點A為圓心,AB長為半徑的圓上,此時點C有無數個,點C的軌跡為圓(不取點B和與A、B共線點),如下圖:②AB=BC,即點C到點B的距離等于點A到點B的距離,則點C在以點B為圓心,AB長為半徑的圓上,此時點C有無數個,點C的軌跡為圓(不取點A和與A、B共線的點),如下圖:
請記住這兩圓一線:
綜上所述,這樣的點C有無數個,點C的軌跡為兩個圓和一條直線,為了方便記憶,我們簡稱“兩圓一線”,這是等腰三角形存在性處理的基本定性策略。
- 嘉成老師解析 -
同學們~碰到一次函數跟幾何結合的題目,等腰三角形的存在性問題時,要想到兩圓一線的方法;每一個點都有可能是定點,所有分3種情況進行討論,其中一種是找垂直平分線,另外兩種是以給定的一個點為圓心,線段長度為半徑,垂直平分線/圓與所給線段的交點,即為所求。
其次,我們來解決第二個問題,等腰三角形的邊長問題。
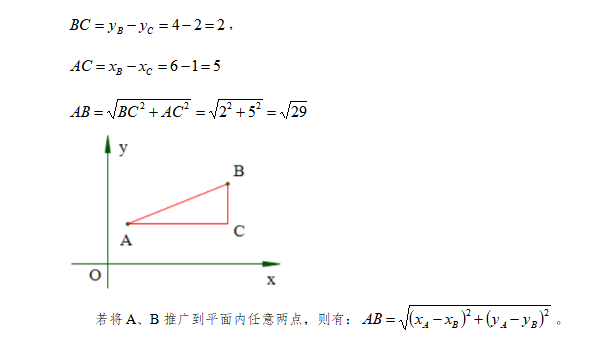
求等腰三角形的邊長,我們通常將其轉化為兩點間的距離問題,所以,我們來推導一下平面內兩點間的距離公式。已知平面內兩點A(1,2)、B(6,4),求線段AB的長度。連接AB,以AB為斜邊,構造直角邊與坐標軸平行的直角三角形,利用勾股定理解題,如下圖:
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2023中考一路陪伴同行!>>點擊查看