來源:網絡資源 2023-07-22 21:18:10
代數式
一、代數式
1、代數式:
用運算符號把數或表示數的字母連結而成的式子,叫代數式。單獨一個數或者一個字母也是代數式。
2、代數式的值:
用數值代替代數里的字母,計算后得到的結果叫做代數式的值。
3、代數式的分類:
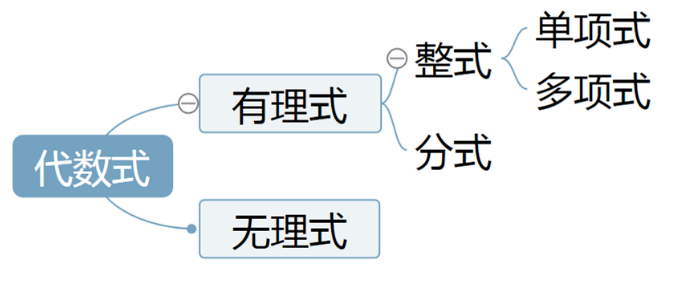
二、整式的有關概念及運算
1、概念
(1)單項式:像x、7、2x2y,這種數與字母的積叫做單項式。單獨一個數或字母也是單項式。
單項式的次數:一個單項式中,所有字母的指數叫做這個單項式的次數。
單項式的系數:單項式中的數字因數叫單項式的系數。
(2)多項式:幾個單項式的和叫做多項式。
多項式的項:多項式中每一個單項式都叫多項式的項。一個多項式含有幾項,就叫幾項式。
多項式的次數:多項式里,次數最高的項的次數,就是這個多項式的次數。不含字母的項叫常數項。
2、運算
升(降)冪排列:把一個多項式按某一個字母的指數從小(大)到大(小)的順序排列起來,叫做把多項式按這個字母升(降)冪排列。(3)同類項:所含字母相同,并且相同字母的指數也分別相同的項叫做同類項。(1)整式的加減:合并同類項:把同類項的系數相加,所得結果作為系數,字母及字母的指數不變。去括號法則:括號前面是“+”號,把括號和它前面的“+”號去掉,括號里各項都不變;括號前面是“-”號,把括號和它前面的“-”號去掉,括號里的各項都變號。添括號法則:括號前面是“+”號,括到括號里的各項都不變;括號前面是“-”號,括到括號里的各項都變號。整式的加減實際上就是合并同類項,在運算時,如果遇到括號,先去括號,再合并同類項。(2)整式的乘除:冪的運算法則:其中m、n都是正整數。同底數冪相乘:am·an=am+n;同底數冪相除:am÷an=am-n;冪的乘方:(am)n=amn;積的乘方:(ab)n=anbn。單項式乘以單項式:用它們系數的積作為積的系數,對于相同的字母,用它們的指數的和作為這個字母的指數;對于只在一個單項式里含有的字母,則連同它的指數作為積的一個因式。單項式乘以多項式:就是用單項式去乘多項式的每一項,再把所得的積相加。多項式乘以多項式:先用一個多項式的每一項乘以另一個多項式的每一項,再把所得的積相加。單項式除單項式:把系數,同底數冪分別相除,作為商的因式,對于只在被除式里含有字母,則連同它的指數作為商的一個因式。多項式除以單項式:把這個多項式的每一項除以這個單項,再把所得的商相加。平方差公式:(a+b)(a-b)=a2-b2;完全平方公式:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2。
三、因式分解
1、因式分解概念:
把一個多項式化成幾個整式的積的形式,叫因式分解。
2、常用的因式分解方法:
(1)提取公因式法:
ma+mb+mc=m(a+b+c)
(2)運用公式法:
平方差公式:
a2-b2=(a+b)(a-b);
完全平方公式:
a2±2ab+b2=(a±b)2
(3)十字相乘法:
x2+(a+b)x+ab=(x+a)(x+b)
(4)分組分解法:將多項式的項適當分組后能提公因式或運用公式分解。
(5)運用求根公式法:
若ax2+br+c=0(a≠0)的兩個根是x1、x2,則有:
ax2+bx+c=a(x-x1)(x-x2)
3、因式分解的一般步驟:
(1)如果多項式的各項有公因式,那么先提公因式;
(2)提出公因式或無公因式可提,再考慮可否運用公式或十字相乘法;
(3)對二次三項式,應先嘗試用十字相乘法分解,不行的再用求根公式法。
(4)最后考慮用分組分解法。
四、分式
1、分式定義:
形如A/B的式子叫分式,其中A、B是整式,且B中含有字母。
(1)分式無意義:B=0時,分式無意義;B≠0時,分式有意義。
(2)分式的值為0:A=0,B≠0時,分式的值等于0。
(3)分式的約分:把一個分式的分子與分母的公因式約去叫做分式的約分。方法是把分子、分母因式分解,再約去公因式。
(4)最簡分式:一個分式的分子與分母沒有公因式時,叫做最簡分式。分式運算的最終結果若是分式,一定要化為最簡分式。
(5)通分:把幾個異分母的分式分別化成與原來分式相等的同分母分式的過程,叫做分式的通分。
(6)最簡公分母:各分式的分母所有因式的最高次冪的積。
(7)有理式:整式和分式統稱有理式。
2、分式的基本性質:
(1)A/B=A·M/B·M
(M是≠0的整式);
(2)A/B=A÷M/A÷M
(M是≠0的整式)
3、分式的運算:
(3)分式的變號法則:分式的分子,分母與分式本身的符號,改變其中任何兩個,分式的值不變。(1)加、減:同分母的分式相加減,分母不變,分子相加減;異分母的分式相加減,先把它們通分成同分母的分式再相加減。(2)乘:先對各分式的分子、分母因式分解,約分后再分子乘以分子,分母乘以分母。(3)除:除以一個分式等于乘上它的倒數式。(4)乘方:分式的乘方就是把分子、分母分別乘方。
五、二次根式
1、二次根式的概念:
式子√a(a≥0)叫做二次根式。
(1)最簡二次根式:被開方數的因數是整數,因式是整式,被開方數中不含能開得盡方的因式的二次根式叫最簡二次根式。
(2)同類二次根式:化為最簡二次根式之后,被開方數相同的二次根式,叫做同類二次根式。
(3)分母有理化:把分母中的根號化去叫做分母有理化。
(4)有理化因式:把兩個含有二次根式的代數式相乘,如果它們的積不含有二次根式,我們就說這兩個代數式互為有理化因式(常用的有理化因式有:√ā與√a,a√b+c√a與a√b-c√a)
2、二次根式的性質:
(1)(√a)2=a(a≥0)
(2)√a2=∣a∣(a≥0)a≥0時,√a2=a
a<0時,√a2=-a
(3)√ab=√a·√b(a≥0,b≥0)(4)√a/b=√a/√b(a≥0,b>0)
3、運算:
(1)二次根式的加減:將各二次根式化為最簡二次根式后,合并同類二次根式。(2)二次根式的乘法:√a·√b=√ab(a≥0,b≥0)(3)二次根式的除法:√a/√b=√a/b(a≥0,b>0)
二次根式運算的最終結果如果是根式,要化成最簡二次根式。
編輯推薦:

歡迎使用手機、平板等移動設備訪問中考網,2025中考一路陪伴同行!>>點擊查看