- 全國站
來源：網絡資源 2023-07-22 21:20:36
方程和方程組
一、方程有關概念
1、方程：
含有未知數的等式叫做方程。
2、方程的解：
使方程左右兩邊的值相等的未知數的值叫方程的解，含有一個未知數的方程的解也叫做方程的根。
3、解方程：
求方程的解或方判斷方程無解的過程叫做解方程。
4、方程的增根：
在方程變形時，產生的不適合原方程的根叫做原方程的增根。
二、一元方程
1、一元一次方程
(1)一元一次方程的標準形式：ax+b=0(其中×是未知數，a、b是已知數，a≠0)
(2)一元一次方程的最簡形式：ax=b(其中x是未知數，a、b是已知數，a≠0)
(3)解一元一次方程的一般步驟：去分母、去括號、移項、合并同類項和系數化為1。
2、一元二次方程
(4)一元一次方程有唯一的一個解。(1)一元二次方程的一般形式：ax2+bx+c=0(其中x是未知數，a、b、c是已知數，a≠0)(2)一元二次方程的解法：直接開平方法、配方法、公式法、因式分解法。(3)一元二次方程解法的選擇順序是：先特殊后一般，如沒有要求，一般不用配方法。
(4)一元二次方程的根的判別式：△=b2-4ac
當△>0時←→方程有兩個不相等的實數根;
當△=0時←→方程有兩個相等的實數根;當△<0時←→方程沒有實數根，無解;當△≥0時←→方程有兩個實數根。(5)一元二次方程根與系數的關系：若x1、x2是一元二次方程ax2+bx+c=0的兩個根，那么：x1+x2=-b/a，x1·x2=c/a。(6)以兩個數x1、x2為根的一元二次方程(二次項系數為1)是：x2-(x1+x2)x+x1·x2=0
三、分式方程
1、定義：
分母中含有未知數的方程叫做分式方程。
2、分式方程的解法：
一般解法：去分母法，方程兩邊都乘以最簡公分母。
特殊方法：換元法。
3、檢驗方法：
一般把求得的未知數的值代入最簡公分母，使最簡公分母不為0的就是原方程的根;使得最簡公分母為0的就是原方程的增根，增根必須舍去，也可以把求得的未知數的值代入原方程檢驗。
四、方程組
1、方程組的解：
方程組中各方程的公共解叫做方程組的解。
2、解方程組：
求方程組的解或判斷方程組無解的過程叫做解方程組
3、一次方程組：
(1)二元一次方程組：
一般形式：
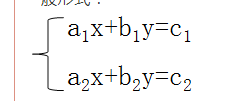
(a1，a2，b1，b2，c1，c2不全為0)
解法：代入消遠法和加減消元法
解的個數：有唯一的解，或無解，當兩個方程相同時有無數的解。
4、二元二次方程組：
(2)三元一次方程組：解法：代入消元法和加減消元法(1)定義：由一個二元一次方程和一個二元二次方程組成的方程組以及由兩個二元二次方程組成的方程組叫做二元二次方程組。
(2)解法：消元，轉化為解一元二次方程，或者降次，轉化為二元一次方程組。
考點與命題趨向分析
（一）一元二次方程的解法
特殊方程：
(1)用直接開方法解;
(2)用公式法;
(3)用因式分解法
[規律總結]如果一元二次方程形如(x+m)2=n(n≥0)，就可以用直接開方法來解;利用公式法可以解任何一個有解的一元二次方程，運用公式法解一元二次方程時，一定要把方程化成一般形式。
一般方程：
(1);先化為一般形式，再用公式法解;
(2)直接可以十字相乘法因式分解后可求解。
[規律總結]對于帶字母系數的方程解法和一般的方程沒有什么區別，在用公式法時要注意判斷△的正負。
（二）分式方程的解法：
分析：(1)用去分母的方法;(2)用換元法解。
[規律總結]一般的分式方程用去分母法來解，一些具有特殊關系如：有平方關系，倒數關系等的分式方程，可采用換元法來解。
（三）根的判別式及根與系數的關系
規律總結1：對于根的判別式的三種情況要很熟練，還有要特別留意二次項系數不能為0。
規律總結2：此類題目可以先解出第一方程的兩個解，但有時這樣又太復雜，用根與系數的關系就比較簡單。
（四）方程組
分析1：(1)用加減消元法消x較簡單;(2)應該先用加減消元法消去y,變成二元一次方程組，較易求解。
[規律總結]加減消元法是最常用的消元方法，消元時那個未知數的系數最簡單就先消那個未知數。
分析2：(1)可用代入消元法，也可用根與系數的關系來求解;(2)要先把第一個方程因式分解化成兩個二元一次方程，再與第二個方程分別組成兩個方程組來解。
[規律總結]對于一個二元一次方程和一個二元二次方程組成的方程組一般用代入消元法，對于兩個二元二次方程組成的方程組，一定要先把其中一個方程因式分解化為兩個一次方程再和第二個方程組成兩個方程組來求解。
編輯推薦：
歡迎使用手機、平板等移動設備訪問中考網，2024中考一路陪伴同行！>>點擊查看
